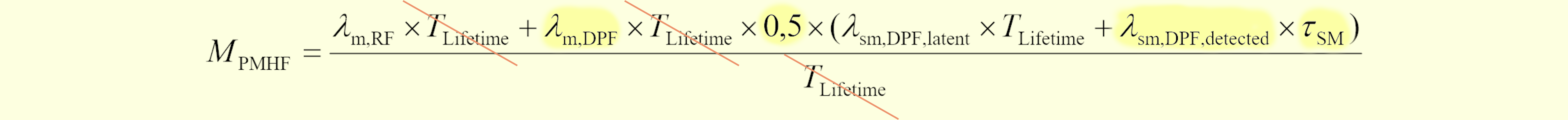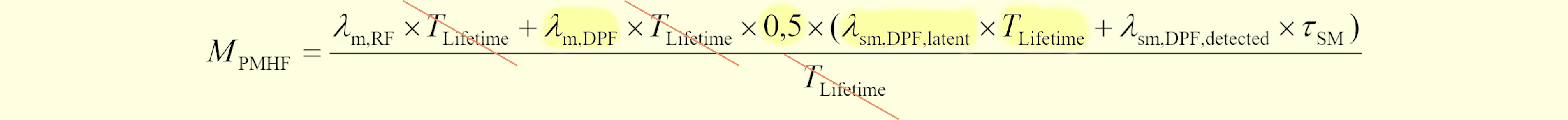パターン2
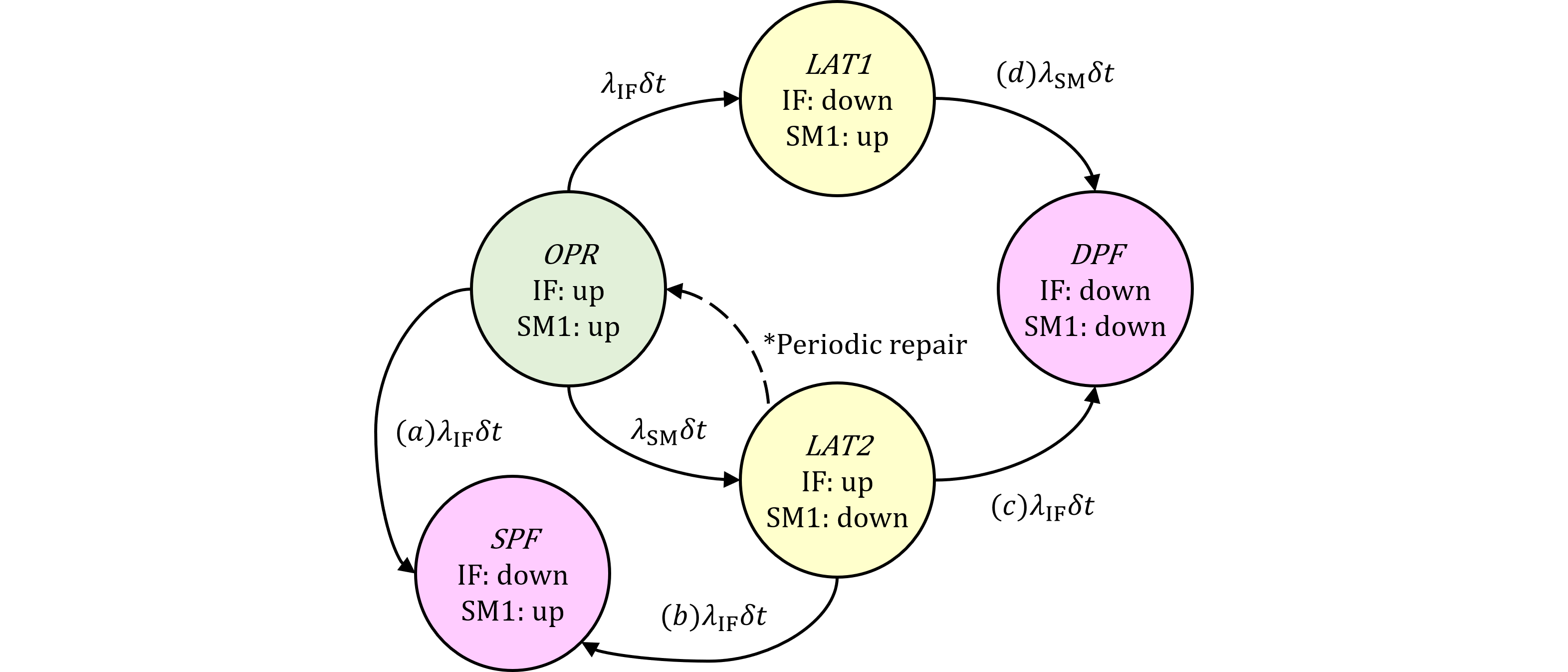
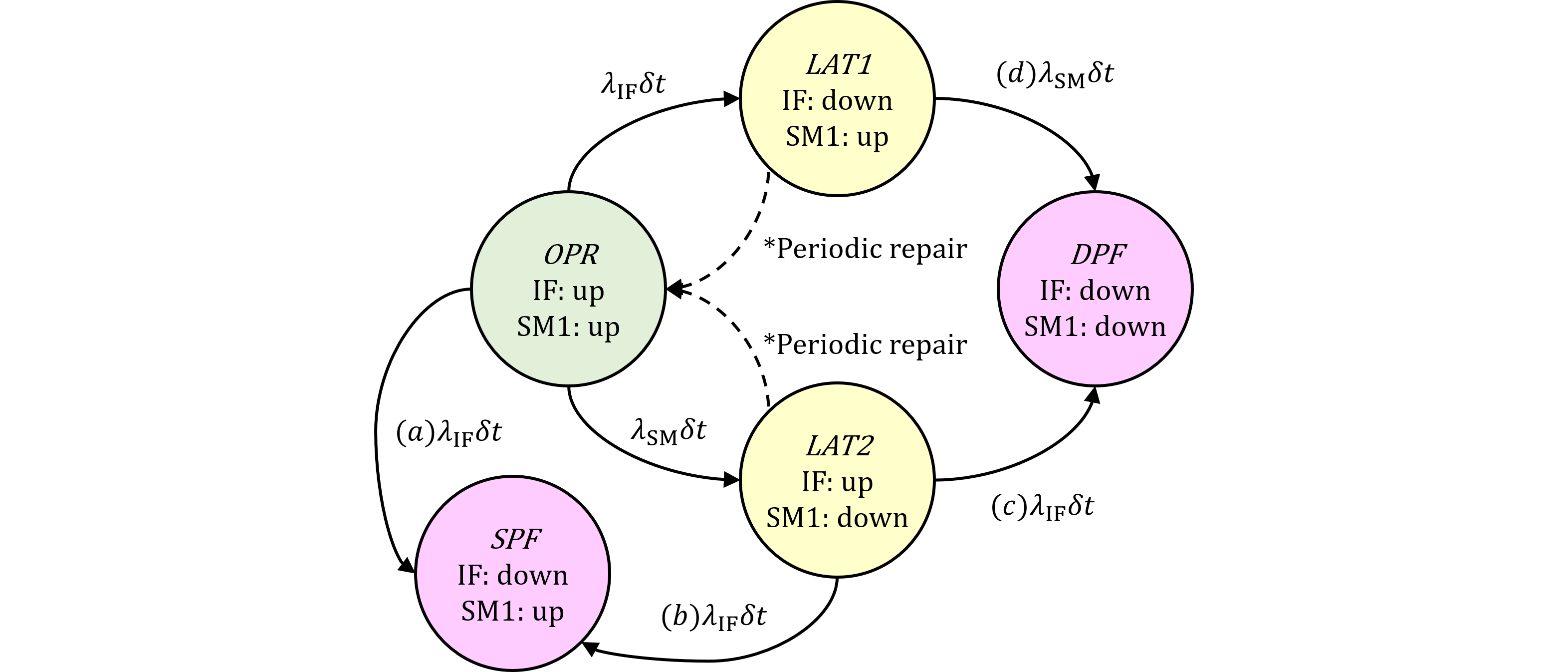
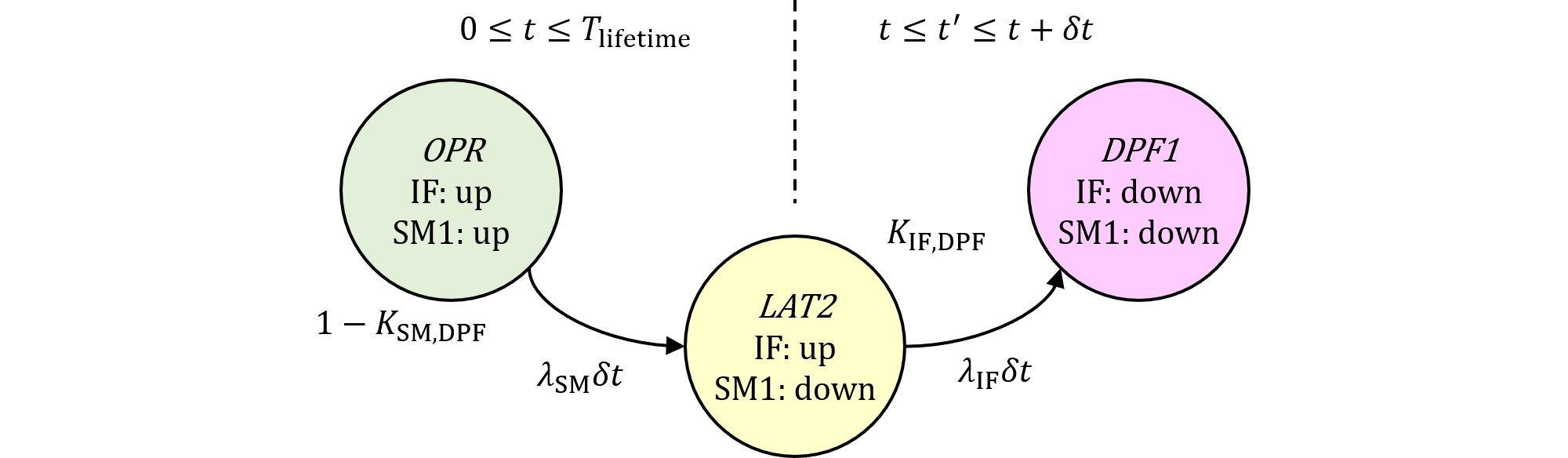
次にパターン2です。図477.1にISO 26262第2版解説書のパターン2の導出過程を引用します。
 図477.1 規格解説書パターン2
図477.1 規格解説書パターン2
解説書で示される導出過程の誤り原因は3つあり、前稿(476.3)で指摘した(マイナーな)2つの他、重大な誤りなのがIFのフォールトの積分範囲です。
図477.1によれば、時刻$t$がSM1のフォールト発生時刻、時刻$t'$が引き続くIFのフォールト発生時刻であり、(477.1)に$t$と$t'$の制約を示します。
$$
\begin{eqnarray}
\begin{cases}
t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime} \\
t': \text{Time of fault of IF}, t\le t'\le \color{red}{t+T_\text{service}}\quad\quad\color{red}{(誤りであるため注意)}
\end{cases}
\end{eqnarray}\tag{477.1}
$$
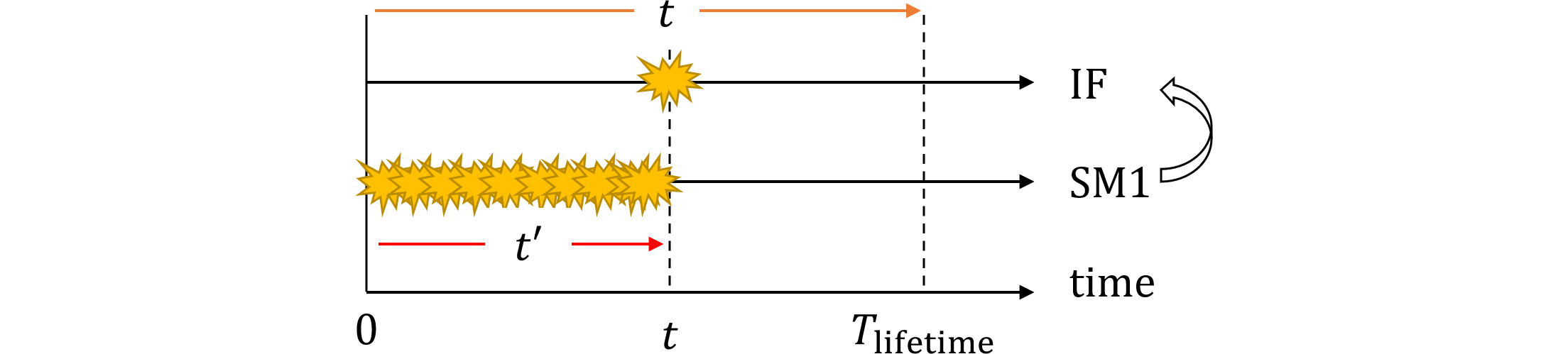
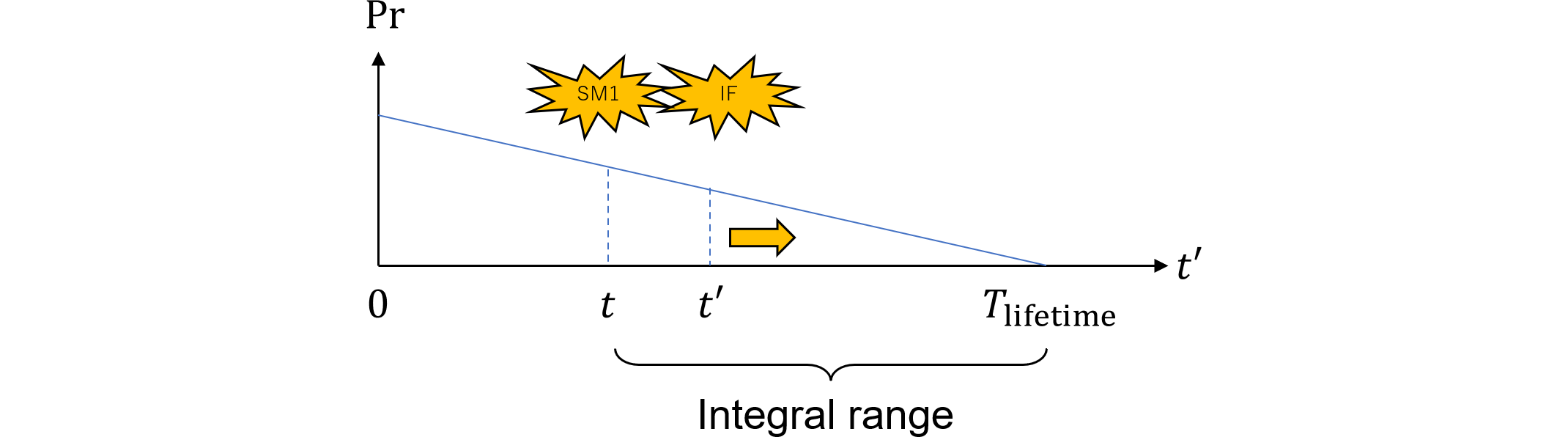
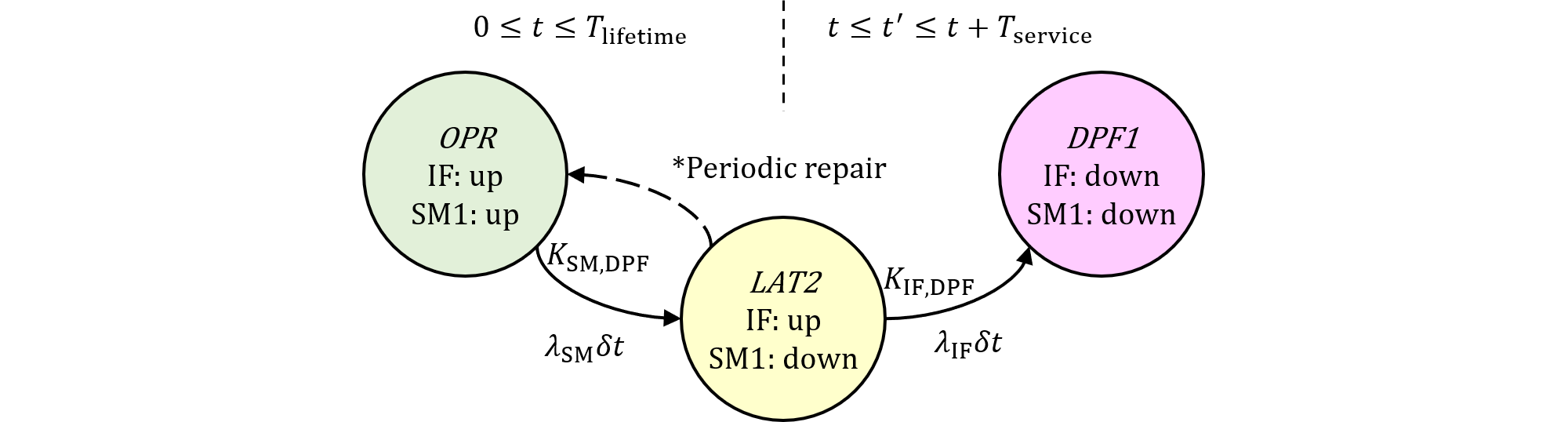
IFのフォールトの積分範囲、つまり$t'$の範囲は$t$から$t+T_\text{service}$となっていますが、図477.2のように、$t$が大となっても積分範囲は常に一定値$T_\text{service}$となることが問題です。
 図477.2 2nd editionパターン2積分範囲(規格第2版)
図477.2 2nd editionパターン2積分範囲(規格第2版)
なぜなら、SM2によるSM1の検査・修理は、SM1のフォールト時点$t$によらず一定周期$T_\text{service}$で実施されるため、図477.2の方法では$t$に依存して暴露終了時刻がズレていきます。暴露終了時刻が$t$に依存しなければ、本来$t'$が$t$から離れるほど、IFのフォールト発生確率は小さくなるはずです。
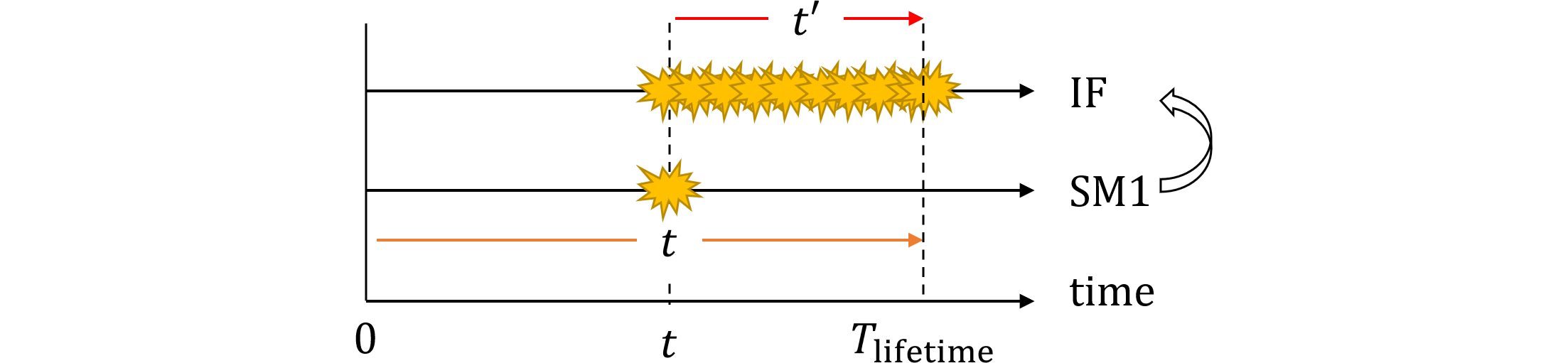
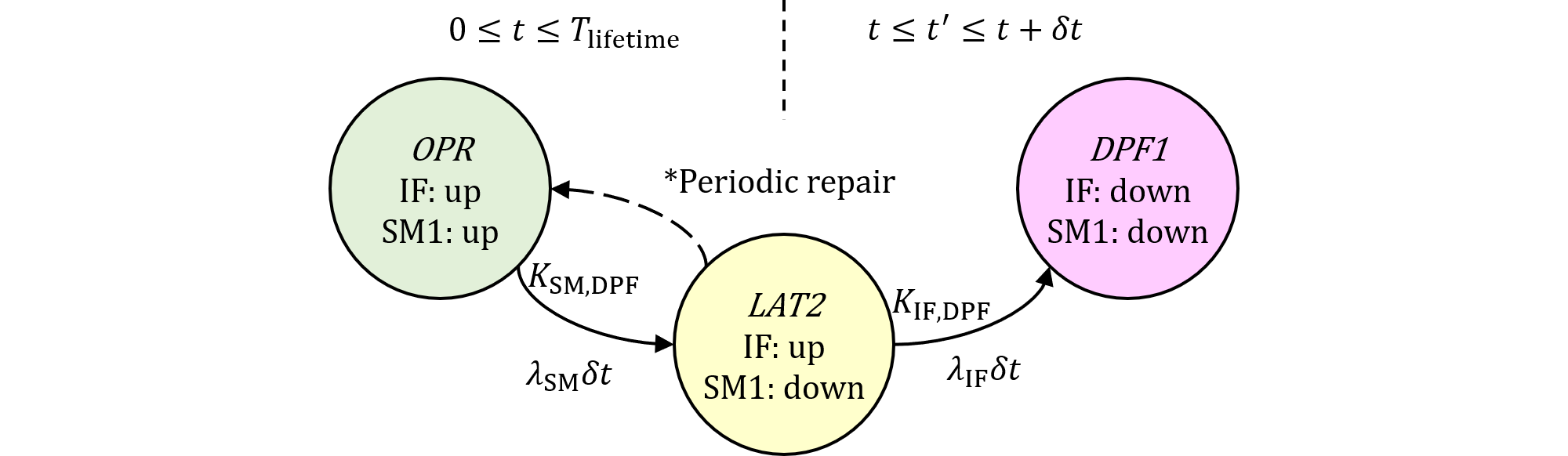
区間$(0, T_\text{lifetime}]$中に検査周期である$T_\text{service}$は$n\equiv\frac{T_\text{lifetime}}{T_\text{service}}$個あります。$i$番目の周期は図477.3のように区間$(iT_\text{service},(i+1)T_\text{service}]$で表され、$t'$はその中でのみ積分されます。従って積分範囲は図477.3のようになるべきです。
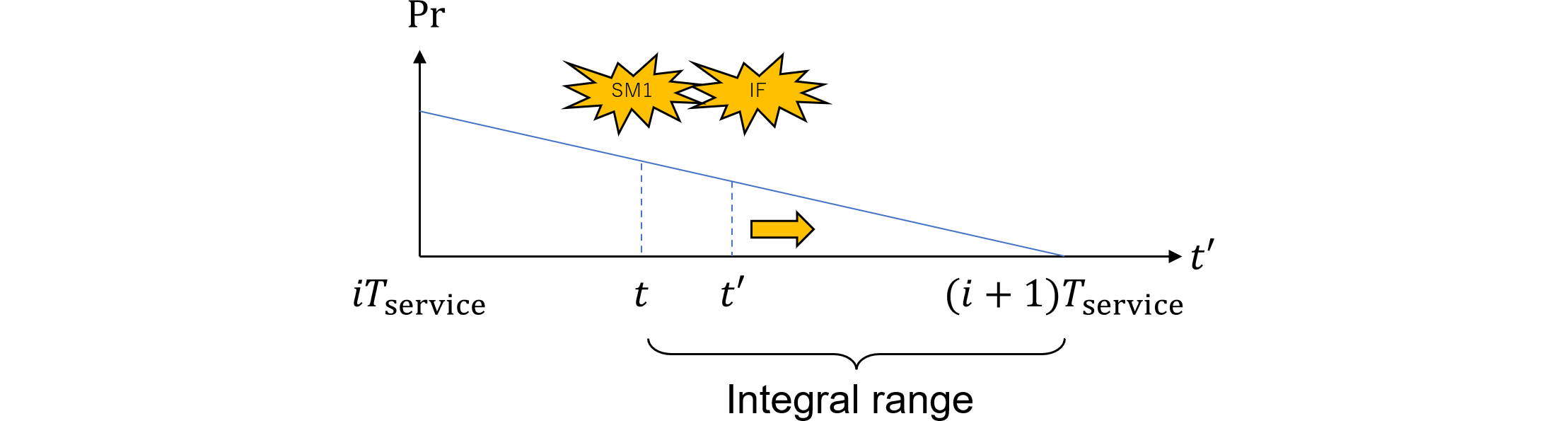 図477.3 2nd editionパターン2積分範囲(修正版)
図477.3 2nd editionパターン2積分範囲(修正版)
従って、$t$と$t'$の制約は(477.2)となります。
$$
\begin{eqnarray}
\begin{cases}
t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime},\ \ s.t.\ \ iT_\text{service}\le t\ \lt(i+1)T_\text{service}\\
t': \text{Time of fault of IF}, t\le t'\le \color{green}{(i+1)T_\text{service}}
\end{cases}
\end{eqnarray}\tag{477.2}
$$
パターン2は、SM2によりSM1のフォールトが検出可能な部分であるため、SM1のフォールトは起きたとしても検査・修理周期内でしかレイテントとなりえません。図477.3のように、$i$番目の検査周期でフォールトが起きたとすれば、$i+1$番目の周期までに修理されることになります。積分範囲はたかだか$T_\text{service}$であり、解説書のように$T_\text{service}$一定値ではありません。
準備ができたので、基本的には規格の流儀で計算しますが、先に誤りを修正します。IFに関する修正点は前稿と同様で、以下の2点です。
$$
\begin{eqnarray}
\begin{cases}
R_\text{IF}(t)&\Rightarrow&R_\text{IF}(t')\quad\quad\text{(up条件)}\\
f_\text{IF,DPF}(t')&\Rightarrow&\lambda_\text{IF,DPF}\quad\quad\text{(down条件)}
\end{cases}
\end{eqnarray}\tag{476.3}
$$
(476.3)及び上記積分範囲の修正を適用し、前稿と同様に(476.4)に対応する式を示せば、
$$
\begin{eqnarray}
&&\Pr\{\text{IF is in }LAT2S\cap\text{IF fails in }[t, (i+1)T_\text{service})\}\\
&=&\Pr\{\text{IF up at }t\cap\text{IF prevented}\cap\text{IF fails in }[t, (i+1)T_\text{lifetime})\}\\
&=&\Pr\{\text{IF prevented}\}\int_t^{(i+1)T_\text{lifetime}}d\!\Pr\{\text{IF down in }[t', t'+dt')\cap\text{IF up at }t'\}\\
&=&K_\text{IF, DPF}\int_t^{(i+1)T_\text{service}}d\!\Pr\{\text{IF down in }[t', t'+dt')\ |\ \text{IF up at }t'\}\cdot\Pr\{\text{IF up at }t'\}\\
&=&K_\text{IF,DPF}\int_t^{(i+1)T_\text{service}}\lambda_\text{IF}R_\text{IF}(t')dt'
=K_\text{IF,DPF}\int_t^{(i+1)T_\text{service}}f_\text{IF}(t')dt'\\
&=&K_\text{IF,DPF}\left\lbrack F_\text{IF}(t')\right\rbrack_t^{(i+1)T_\text{service}}
=K_\text{IF,DPF}\left[F_{\text{IF}}((i+1)T_\text{service})-F_\text{IF}(t)\right]\\
&\approx&K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)
\end{eqnarray}\tag{477.3}
$$
と表せます。前稿で述べたように解説書の2か所の誤りが確認できます。
(477.3)により$t$におけるIFの車両寿命までのフォールト確率を表せました。$t\le t'$の条件下ではSM1とIFのフォールトの生起確率は独立として掛け合わせることができます。従って$t$を周期的な変数$u\equiv t \bmod T_\text{service}$とその逆の関係である$t=iT_\text{service}+u, i=0, 1, 2, ..., n-1$で表せば、パターン2のPMHFは、
$$
\begin{eqnarray}\require{cancel}
M_\text{PMHF,P2}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{SM1 down in }[t, t+dt)\cap\text{SM1 detected}\\
&&\cap\ \text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}\\
&=&\frac{1}{T_\text{lifetime}}\Pr\{\text{SM1 detected}\}\sum_{i=0}^{n-1}\int_{iT_\text{service}}^{(i+1)T_\text{service}}d\!\Pr\{\text{SM1 down in }[t, t+dt)\ |\ \\
&&\text{SM1 up at }t\}\Pr\{\text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}\\
&=&\frac{1}{T_\text{lifetime}}K_\text{SM1,DPF}\sum_{i=0}^{n-1}\int_{iT_\text{service}}^{(i+1)T_\text{service}}\lambda_\text{SM1}R_\text{SM1}(t)\\
&&\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}dt
\end{eqnarray}\tag{477.4}
$$
ここで、等比級数の公式と、$x\ll1$の際のマクローリン近似$e^{-x}\approx1-x$を用いて、
$$
\begin{eqnarray}\require{cancel}
&=&\frac{1}{T_\text{lifetime}}n K_\text{SM1,DPF}K_\text{IF,DPF}\int_0^{T_\text{service}}\lambda_\text{SM1}R_\text{SM1}(u)\lambda_\text{IF}\left(T_\text{service}-u\right)du\\
&=&\frac{1}{\bcancel{T_\text{lifetime}}}\frac{\bcancel{T_\text{lifetime}}}{T_\text{service}}K_\text{SM1,DPF}K_\text{IF,DPF}\int_0^{T_\text{service}}f_\text{SM1}(u)\lambda_\text{IF}\left(T_\text{service}-u\right)du\\
&\approx&\frac{1}{\bcancel{T_\text{service}}}K_\text{SM1,DPF}K_\text{IF,DPF}\lambda_\text{IF}\lambda_\text{SM1}\left\lbrack T_\text{service}\bcancel{u}-\frac{1}{2}u^\bcancel{2}\right\rbrack_0^{T_\text{service}}\\
&=&\frac{1}{2}K_\text{IF,DPF}K_\text{SM1,DPF}\lambda_\text{IF}\lambda_\text{SM1}T_\text{service}\\
&=&\frac{1}{2}\lambda_\text{SM1,DPF,det}\lambda_\text{IF,DPF}T_\text{service}
\end{eqnarray}\tag{477.5}
$$
となります。なお、式変形中に弊社積分公式(471.3)を使用しています。
結果の(477.5)と、次の図477.4に引用する規格第2版式のパターン2を比較すると、規格式の値は2倍大きく、これは前述のとおりIFのフォールトに関する積分範囲が過剰なことに因るものです。
 図477.4 規格第2版式(パターン2をハイライト)
図477.4 規格第2版式(パターン2をハイライト)
一方、(477.5)は次の図477.5に引用する規格初版式のパターン2に相当する部分(黄色部分)と(IF⇒m, $T_\text{service}$⇒$\tau_\text{SM}$と読み替えることにより)正確に一致します。
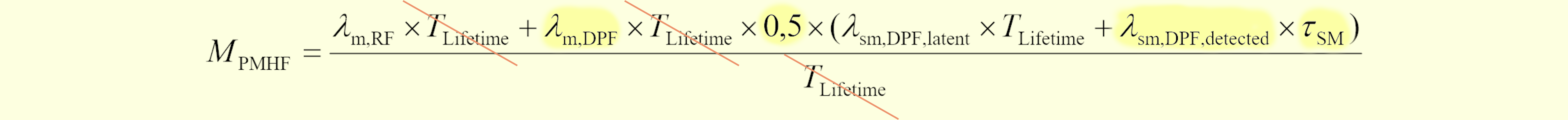 図477.5 規格初版第1式(パターン2をハイライト)
図477.5 規格初版第1式(パターン2をハイライト)
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。
 前のブログ
次のブログ
前のブログ
次のブログ